排列组合——最常用的7种计数方法
排列组合——最常用的7种计数方法
排列组合——最常用的7种计数方法
老徐写在前：
很多同学在学习数据分析这一模块后，都有一个共同的感觉，那就是“难”，“难”，“难”，老徐觉得，之所以给人的感觉是难，主要原因还是这一模块的题目灵活多变，好像给人的感觉是每一个题目都是自己没有学过的。
但是，其实我们还是没有掌握其精髓，所以老徐今天这篇文章，就给大家总结一下排列组合最常用的7种计数方法以及其解题关键点。
如果对你有帮助，请点赞。
一、穷举法（枚举法）
适合题目类型：
①答案选项数字偏小或者题目中总数较小——10个左右；
②骰子问题。
（一枚骰子6种情况，2枚骰子36种情况）
注意事项：
枚举法是最简单也是最容易出错的方法，所以在枚举时要按照一定的规律去列举，切不可想到一种列一种，这样容易列少或者列多。
举例：
【巩固练习】（答案在文章最底部留言处）
二、捆绑法
适合题目类型：
“相邻”或“在一起”的排列组合问题
注意事项：
对于某几个要求相邻的排列组合问题，可将相邻的元素看做一个“元”与其他元素排列，然后对“元”的内部进行排列。
举例：
【巩固练习】（答案在文章最底部留言处）
三、插空法
适合题目类型：
“不相邻”或“不在一起”的排列组合问题
注意事项：
对于某几个元素不相邻的排列问题，可先讲其他元素排好，再将不相邻的元素在已排列好的元素之间空隙中及两端插入即可。
举例：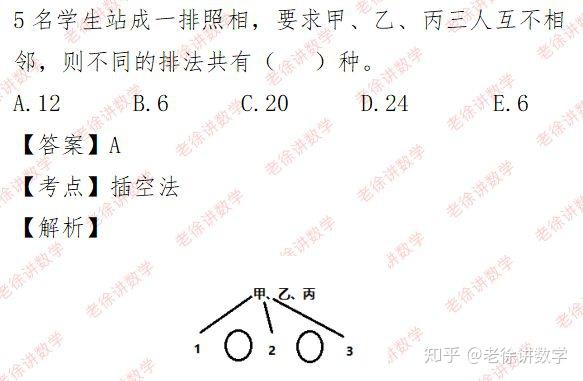
【巩固练习】（答案在文章最底部留言处）
四、隔板法
适合题目类型：
处理相同的东西分给不同的人，每人至少一个的排列组合问题。
注意事项：
隔板法就是在n个元间的n-1个空中插入若干个隔板，可以把n个元素分成（n+1）组的方法，应用隔板法必须满足三个条件：
（1）这n个元素必须互不相异；
（2）所分成的每一组至少分得一个元素；
（3）分成的组彼此相异。
基本公式：n个元素产生n-1个空，分成m组，插入m-1块板，所以总数为
。
举例：
【巩固练习】（答案在文章最底部留言处）
五、分组除序法
适合题目类型：
处理不同的元素分给不同的组的排列组合问题。
注意事项：
不同的元素分给不同的组，如果有出现人数相同的这样的组，并且该组没有“名称”，则需要除序，有几个相同的就除以几的阶乘，如果分的组有名称，则不需要除序。
举例：
【巩固练习】（答案在文章最底部留言处）
六、特殊元素优先安排
适合题目类型：
对于带有特殊元素的排列组合问题，一般应先考虑特殊元素，再考虑其他元素。
注意事项：
根据题目找到“特殊元素”，这才是解题的切入点。
举例：
【巩固练习】（答案在文章最底部留言处）
七、正难反易法
适合题目类型：
对于一些直接求解较为复杂的问题，从正面入手很难解决，这时可从反面入手，从而将其转化为一个简单的问题来处理。
注意事项：
要能够准确的找到一些问题的反面，比如“至少一个”的反面是“一个都没有”等等。
举例：
【巩固练习】（答案在文章最底部留言处）
注意本题是豪华游5种。
以上内容来源于微信公众号《老徐讲数学》，答案在微信公众号上公布，如有问题请联系老徐。
排列组合——最常用的7种计数方法
Comments
Post a Comment